I’m generally disappointed when I come across source code examples for multiprocessing technologies that use trivial algorithms to demonstrate the simplicity of an implementation. This not only establishes expectations that are unrealistic but also hides details that are painfully discovered when applied to more complex code. We are after all, trying to improve performance in our real-world applications with multiprocessing by targeting algorithms that have a real impact on the end user, which probably does not include a bubble sort.
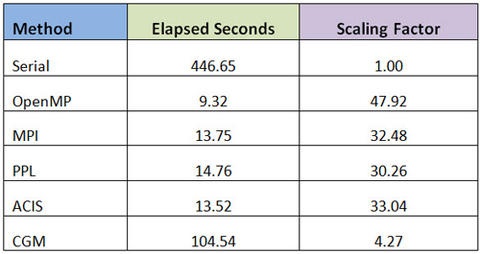
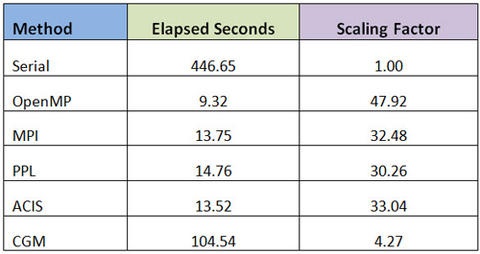
As mentioned in my previous post, I have a new toy with 48 cores and thought it would be interesting to put the various multiprocessing technologies that are at my disposal to the test. These are: OpenMP, MPI, PPL (Microsoft Concurrency Runtime), the ACIS thread manager, and the CGM multiprocessing infrastructure. Forgive me for creating yet another trivial example, but finding prime numbers is simple and yet compute intensive, and serves my purpose well. The challenge is to find the number of primes between 1 and 100,000,000 as quickly as possible. I’m using Visual Studio 2010 when possible, targeting 64 bit release binaries. Here are the results:
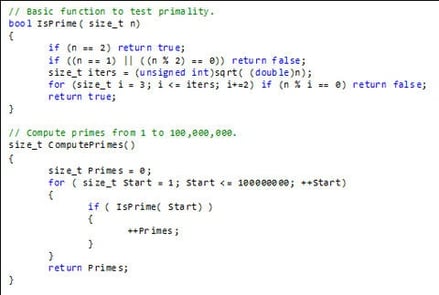
Before evaluating the results, let’s first have a look at the implementation. I’m not going to show all of the code but instead just focus on the highlights. Let’s start with the original implementation used to calculate the serial time. As we can see, the iterations of the loop test for primality and conditionally increment a total. I’ve included the IsPrime function (in a simplified format) just to show that it is reentrant. This function is thread-safe because it does not modify or maintain state data, and will therefore not have any side effects.
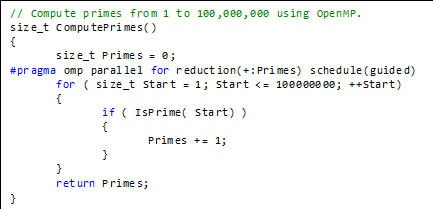
The OpenMP version only requires one additional line of code to add parallelism. The pragma statement instructs OpenMP to parallelize the loop, to create a thread-local version of Primes to be summed up at the end, and to schedule the iterations using a guided approach. The syntax is quite simple and is explained in more detail on Wikipedia.
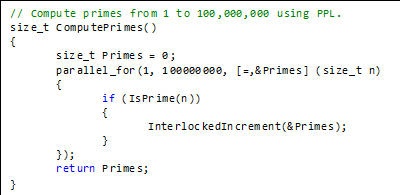
The PPL version also requires only minor changes. I used the parallel_for statement from the Parallel Patterns Library, which is part of the Microsoft Concurrency Runtime. This version takes a start and end value, and a lambda expression, which consists of a capture clause, a parameter list, and a function body. A more thorough explanation can be found on the MSDN website. The Windows kernel function InterlockedIncrement avoids race conditions by incrementing the Primes variable atomically.
The other three implementations (ACIS, CGM, and MPI) are not as trivial because we have to divide the work into smaller pieces, typically into one task for each processor. So we divide up the range into 48 pieces and let each process/thread calculate the number of primes in their sub-range. Then we add all the answers together. The ACIS implementation is shown below.
Part I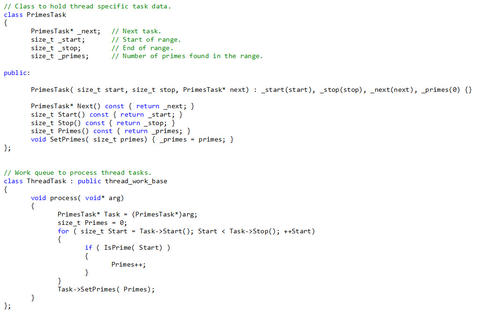
Part II
In terms of simplicity and performance, OpenMP is the clear winner. It achieved almost perfect scaling and the implementation is simple and straightforward. PPL is a close second, requiring very few changes to original code with good scalability. The syntax is a bit difficult to understand at first but lambda expressions are the new thing. So much so that they are included in the next C++ standard.
The downfall of these two approaches is that they do not allow the developer to have any control of the threads that are used. When used in ACIS operations, each thread must initialize and terminate the modeler appropriately. Since we do not know which threads will be used by OpenMP and PPL, we must make sure they have properly initialized ACIS in every iteration of the loop. This will certainly have an impact on performance and explains why the ACIS thread manager maintains a pool of pre-initialized threads.
The ACIS and MPI implementations are close in performance and similar in implementation. This is not surprising because the main drawback when using multiple processes is in the overhead of inter-process communication. This is not an issue in the primes example because we are sending two integers to each process (start and stop values) and are receiving one back (the number of primes found in the range). When used in geometric modeling code, this can be a bottleneck.
The CGM results are not what I expected but it’s a bit unfair to be critical at this point. I did after all make significant changes to ACIS in order to handle more than eight threads concurrently. This work has simply not yet been done in CGM. These types of tests put the magnifying glass on the infrastructure, and in the CGM case has exposed additional overhead in creating processes, loading DLLs, and processing the task queue. Things to address in time.


.jpg?width=450&name=Application%20Lifecycle%20Management%20(1).jpg)














