例えば、あなたが航空宇宙技術者で、新しいタイプのジェットエンジンの設計に素晴らしいアイデアを持っているとします。 しかし、最大の出力と最小の燃料消費量を実現するためには、どのようなサイズ、形状、素材の部品を使用すればよいのか、また、あらゆる動作条件で発生する可能性のある様々な熱的・機械的応力の下で破損しないようにするにはどうすればよいのか、わからないとします。また、全く新しいデザインであるため、過去のデザインのデータはなく、ゼロからのスタートだとします。
ひとつの方法としては、経験則から推測して試作品を作り、それをテストすることです。期待していた出力や燃費が得られなかったり、装置が故障したりした場合は、設計を調整して再挑戦します。
この方法の問題点は、コストと時間がかかることと、試作品が粉々に吹き飛んでしまった場合、その原因を正確に特定するのが難しいことです。
もっと良い方法があります。試作品のコンピュータモデルを作り、その動作をシミュレートするのです。設計の変更は、いくつかの数値パラメータを変更するだけで済みますし、もし壊れてしまっても、どのように故障したのかを正確に判断することができます。また、飛んできた試作品の破片に当たることもありません。
コンピュータによるモデリングやシミュレーションには、もちろん課題があります。たくさんの方程式が必要です。部品に使われている素材は、温度が上がるとどのように膨張するのか？それが各部品の形状にどう影響するのか。その結果、部品の周りの空気の流れやエンジンの効率にどのような影響を与えるのか？といった具合です。
方程式の数や複雑さは、通常の方法では解けないほどになります。
幸いなことに、数十年前（コンピュータが普及する前）から、非常に頭の良い人たちがこの問題に取り組むために「ガラ―キン法」と呼ばれる手法を使っていました。モデル全体の方程式を導き出して解くのではなく、モデルを小さなピースに分解して、それぞれのピースに対してよりシンプルな方程式を解き、それぞれのピースの解をまとめて最終的な解を導き出したのです。
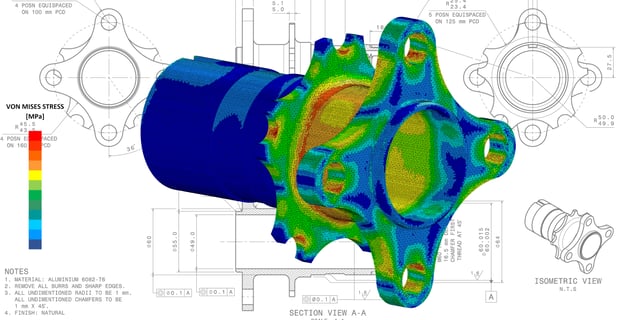
この手法を有限要素モデリング（Finite Element Modeling：FEM）といいます。FEMで作成されたモデルを解析することを有限要素解析（Finite Element Analysis：FEA）といいます。この記事では、FEMの概念と、現実世界のさまざまな問題を解決するためにFEMがどのように使われているかを紹介します。
FEMは最も基本的な形では、複雑な問題空間（ドメイン）を、比較的簡単な方程式で動作を記述できる多数の小さくて単純な部分（有限要素）に分割する近似法です。
FEMはもともと、機械工学、土木工学、航空工学などの複雑なシステムをモデル化して解析するために開発された工学解析用のソフトウェアです。FEMは、ニュートンの運動法則、質量とエネルギーの保存、平衡、熱力学の法則など、力学の基本的な概念を基礎としています。
FEMは、例えば、異なる負荷条件の下での橋の異なる部分の構造力学、エンジン部品を通る熱の流れ、アンテナからの電磁放射の分布などを決定するために使用することができます。
FEMでは、領域をどのように細分化するかが重要なポイントとなります。その点、コンピューター支援設計（CAD）ソフトウェアは、オブジェクトの3次元形状を定義し、目的のメッシュまたは要素を定義する3次元グリッドに従って、オブジェクトを適切なサイズの要素に簡単に分割できるため便利です。メッシュは、解決すべき問題に応じて、立方体やピラミッドのような均一なサイズと形状の要素を定義したり、ドメインの異なる部分に異なる形状とサイズの要素を配置したりすることができます。
適切なメッシュ（要素モデル）を選択することが重要です。粗いメッシュ（細分化が大きい）では精度の低い結果となりますが、細かいメッシュでは要素数が多くなり、解答に必要な計算能力が高くなります。そのため、ドメイン全体でメッシュサイズを変化させることが有効です。あまり関心のない領域には粗いメッシュを定義し、システムの動作に強い影響を与える領域には細かいメッシュを定義することができます。
ある領域をモデリングする際には、解析対象となる部品の材料特性を知ることも重要です。 問題の種類にもよりますが、正確な結果を得るためには、熱膨張係数、電気・熱伝導率、摩擦、誘電率、圧縮・引張強度、降伏応力などの物理的パラメータをモデルに組み込む必要があります。FEMに対応した高度なCADパッケージでは、これらのパラメータをモデルに組み込む方法が用意されています。
FEMの強みは、偏微分方程式（PDE）を扱うことができる点にあります。PDEは、流体の流れや熱伝導、重力の影響など、複数の変数が関係する現象を記述するのに便利ですが、難解で複雑な数学を必要とします。しかし、1つのシステムを記述するために複数のPDEが必要になると、解くのが困難になったり、不可能になったりすることがあります。
PDEを、より扱いやすい代数関係（「定常状態」または平衡状態にあるシステムの場合）または常微分方程式（時間的に変化するシステムの場合）に単純化するには、主に有限差分解析と変分法の2つのアプローチが用いられます。
エネルギー最小化とは、システムのすべての可能な構成の中で、最も安定した構成は、システムの位置エネルギーが最小になる構成であるという考えです。最小エネルギー条件を定義する方程式を知ることで、「弱形式」方程式の定義が可能になります。これは、関係の不連続性、つまり各要素が個別に分析されるシステムに固有の不連続性を許容するためです。
この弱形式方程式は、離散化により、システムの各要素に1つずつの行列方程式に変換されます。この行列式は、2つの数値計算手法のうちの1つを用いて解かれます。
要素ごとに方程式を解くのは良いのですが、それではギャップが生じてしまいます。例えば、各要素の温度は解けても、隣接する要素の温度は同じではないかもしれません。任意に定義された要素の間で温度が段階的に変化することはありえず、現実にはある点と別の点の間には連続的な勾配が存在します。
これらの未知の関数（または自由度）を要素間で近似するには、隣接する要素間のステップ変化と実際の関数との誤差を推定する必要があります。この誤差の推定値を最小にするモデルが、ドメインの実際の状態に最も近似したモデルとなります。
FEAは主に3つのタイプの問題に適用できます。
長年にわたり、特定のタイプの問題に対処するために、いくつかの「フレーバー」のFEAが開発されてきました。
FEMの利用は、かつては計算に必要なスーパーコンピュータを購入できる土木や航空宇宙分野の大規模な大学や研究機関に限られていた。しかし最近では、より高性能で安価なコンピューターが登場したことや、CADソフトなどの開発により、さまざまな産業分野でFEMが採用され、問題解決の幅が広がってきています。
また、燃料電池、新型蓄電池、風力発電機、次世代電動機など、地球温暖化防止のために必要なデバイスの設計にもFEMが活用されています。
FEMやFEAの用途が拡大するにつれ、様々なニッチなアプリケーションでこれらの技術の精度を高めるために、さらなる開発が必要になります。また、より使いやすく、より高速なソフトウェアツールも必要になるでしょう。このように、FEMは新しい分野でも従来の分野でも、爆発的に普及する可能性を秘めているのです。
多くの場合、市場に出回っているアプリケーションは、あなたの特定のニーズに対してあまりにも一般的すぎるかもしれません。まず始めに、問題となる空間を正確にモデリングするための3D Geometry Modelerが必要です。また、多くの場合、シミュレーションしたいデザインはCATIAやSolidworksなどのCADアプリケーションで作成されます。
これらのモデルをアプリケーションにインポートするには、CAD相互運用性ツールキットが必要です。3Dモデラーの自動フィーチャー認識・除去機能、ブーリアン演算機能、BRep変形機能を活用することで、ユーザーの作業を非常に簡単にすることができます。
学生時代のシミュレーション課題では、最初は簡単に終わったように見えても、モデルに不要な穴やフィレットが多すぎてシミュレーションが遅くなり、手動で削除しなければならず、結局何日もかかってしまったことを誰もが覚えているはずです。最後に、FEMアプリケーションで最も重要なコンポーネントの1つがメッシャーです。優れたメッシャーは、3Dモデルの不正確さを処理し、信頼性の高い結果を安定して得ることができます。
ACIS, 3DScript and SAT are registered trademarks of Spatial Corp.
No Comments Yet
Let us know what you think