- What do you do?
- What Exactly is FEM?
- What You Need to Know About Choosing a FEM Modeler
- FEM and Partial Differential Equations
- Finite Element Analysis
- Who Uses FEM?
- How to start building an FEM application?
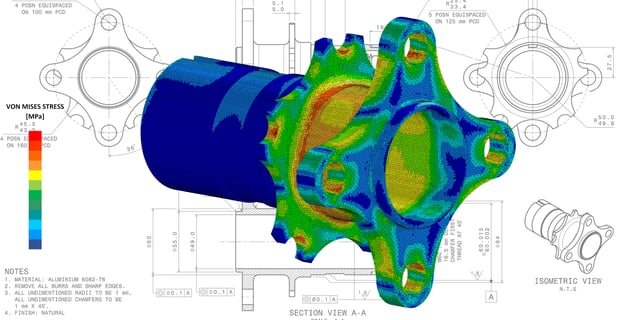
Suppose you’re an aerospace engineer with a great idea for a new type of jet engine design, but you don’t know the sizes, shapes, and materials to use for the parts that will give you maximum power output with minimum fuel consumption, and that won’t break under the various thermal and mechanical stresses likely to be seen over all possible operating conditions. And because the design is totally new, you have no data from previous designs to draw upon—you’re starting from scratch.
What do you do?
One approach would be to make educated guesses, build a prototype, and test it. If you don’t get the power output or fuel economy you were hoping for, or if the device fails, you tweak the design and try again.
The problem with this approach is that it’s expensive and time consuming, and if your prototype blows itself to smithereens, it’s difficult to determine exactly how it failed.
There is a better way: Build a computer model of your prototype and simulate its operation. Tweaking the design is a matter of changing some numerical parameters, and if it breaks, you can determine exactly how it failed. And nobody gets hit by flying prototype shrapnel.
Computer modeling and simulation are not without their challenges, of course. You need lots of equations. How does the material used in the parts expand as its temperature rises? How does that affect the shapes of the various parts? How does that, in turn, affect the airflow around the parts and the efficiency of the engine? And so on.
The number and complexity of the equations can become so great that they are impossible to solve using normal means.
Fortunately, starting a few decades ago—even before computers came into widespread use—some very smart people used a technique called the Galerkin method to tackle this problem. Instead of attempting to derive and solve the equations for the model as a whole, they broke down the model into little pieces and solved the much simpler equations for each piece, then put the solutions for each piece together to reach a final solution.
This approach is called finite element modeling (FEM). Analyzing a model created with FEM is called finite element analysis, or FEA. (The two terms, FEM and FEA, are often used interchangeably.) This article introduces the concepts of FEM and how it’s used to solve a wide variety of real-world problems.

What Exactly is FEM?
In its most basic form, FEM is an approximation method that subdivides a complex problem space, or domain, into numerous small, simpler pieces (the finite elements) whose behavior can be described with comparatively simple equations.
FEM was originally developed for engineering analysis to model and analyze complex systems in mechanical, civil, and aeronautical engineering. It has as its foundation the basic concepts of mechanics, such as Newton’s laws of motion, conservation of mass and energy, equilibrium, and the laws of thermodynamics.
FEM can be used, for example, to determine the structural mechanics of different parts of a bridge under different loading conditions, the heat flow through an engine part, or the distribution of electromagnetic radiation from an antenna.
An important aspect of FEM is how the domain is subdivided. Computer-aided design (CAD) software is useful in this regard, because it defines the three-dimensional shape of an object and can easily subdivide the object into appropriately sized elements according to the desired mesh, or three-dimensional grid that defines the elements. Depending on the problem to be solved, the mesh can define elements of uniform size and shape (such as cubes or pyramids), or can have elements of different shapes and sizes in different parts of the domain.
What You Need to Know About Choosing a FEM Modeler
Choosing the right mesh, or element model, is important: A coarser mesh (larger subdivisions) results in less-accurate results, but a finer mesh, which creates more elements and takes more computing power to solve. That’s why a mesh size that varies across the domain is useful; you can define a coarser mesh in areas that are of less interest, and a finer mesh in areas that have a strong impact on the system behavior.
When modeling a given domain it’s also important to know the material properties of the components being analyzed. Depending on the type of problem, physical parameters such as the coefficient of thermal expansion, the electrical and thermal conductivity, friction, dielectric constants, compressive and tensile strength, yield stress, and more must be incorporated into the model in order to achieve accurate results. Advanced CAD packages that are capable of FEM have ways to incorporate these parameters into the model.

FEM and Partial Differential Equations
The strength of FEM lies in its ability to deal with partial differential equations (PDEs). Without getting into the arcane complex math involved, PDEs are useful in describing phenomena involving multiple variables, such as fluid flow, heat transfer, and the effects of gravity. The trouble is that when you need several interdependent PDEs to describe a system, they become difficult or impossible to solve.
Two main approaches are used to simplify PDEs into more tractable algebraic relationships (for systems in “steady state,” or equilibrium) or ordinary differential equations (for systems undergoing changes over time): finite difference analysis and variational methods.
- Finite difference analysis approximates the derivatives driving the PDEs by use of finite difference equations.
- Variational methods are more commonly used in FEM and are based on the principle of energy minimization.
Energy minimization is the idea that of all the possible configurations of a system, the most stable configuration will be the one in which the system’s potential energy is the smallest. Knowing the equations that define the minimum-energy condition enables the definition of “weak form” equations, so called because they allow for discontinuities in the relations—discontinuities that are inherent in a system in which each element is analyzed separately.
The weak form equations, in turn, enable discretization—conversion to a set matrix equations, one for each element in the system. The matrix equations are then solved by one of two numerical methods:
- Direct solver: The matrix equations lend themselves to calculation of a solution in one pass.
- Iterative solver: The equations are solved through an iterative approximation process that is repeated until a certain parameter falls below a defined threshold.
Solving the equations for each element is all well and good, but it leaves a gap: You might solve, for example, the temperature at each element, but the temperature in adjacent elements might not be the same. It’s unlikely that there is a step change in temperature between these arbitrarily defined elements; in real life, there’s a continuous gradient between one point and another.
Approximating these unknown functions (or degrees of freedom) between elements involves estimating the error between the step change between adjacent elements and the actual function. A model that minimizes this error estimation is one that most closely approximates the actual state of the domain.
Finite Element Analysis
FEA can be applied to three main types of problems:
- Static: For example, structural analysis of different parts of a building or bridge when a certain load is applied with no motion involved. Knowing what parts experience the highest stress tells the designers what parts need to be strongest.
- Dynamic: Useful when the forces applied to the system change over time, for example, heat flow through a system component.
- Modal: Useful in analyzing the effects of vibration on a system.
Over the years, several “flavors” of FEA have been developed to address specific types of problems:
- Extended FEM: This method is useful when analyzing systems with discontinuities, such as fractures; for example, how a system behaves when one of its components has a crack or other defect.
- Generalized FEM: Combines traditional mesh-based FEM with more advanced “meshless” methods.
- Mixed FEM: Useful for problems involving contact between moving parts.
- hp-FEM: Used when certain elements in a system are further subdivided (in a process called mesh refinement), and the polynomial equations of each element have different orders.
- Discontinuous Galerkin FEM: Used to analyze systems in which components can bend or flex.
Who Uses FEM?
The use of FEM was once limited to large universities and research institutes in fields such as civil engineering and aerospace that could afford the supercomputers needed to perform the calculations. More recently, however, more-powerful and less-expensive computers have become available, and developments in CAD software and other tools have led to the adoption of FEM in a wide variety of industries to address an ever-increasing range of problems:
- Automobile manufacturers, appliance manufacturers, and other companies that rely on sheet metal fabrication are turning to FEM to model phenomena such as springback. This enables them to design their fabrication tools to maximize the precision of the finished products.
- Telecommunications equipment manufacturers are using FEM to optimize antenna designs for 5G cellular base stations, mobile devices, and other equipment.
- Aerospace companies such as SpaceX and Blue Origin use FEM in the design of their advanced rocket engines.
FEM can also be used to design devices such as fuel cells, advanced electric storage batteries, wind turbines, and next-generation electric motors that are needed to meet the world’s carbon-reduction needs.
As the uses of FEM and FEA expand, more development will be needed to increase the accuracy of these techniques in various niche applications. Software tools that are easier to use and feature faster performance will be needed as well. FEM is thus poised for explosive growth in its application in both new and traditional fields.
How to start building an FEM application?
A lot of times, the applications on the market may be too generic for your specific needs. To get started, you will need a 3D Geometry Modeler to accurately model the problem space. Also, more often than not, the designs you want to simulate are created in CAD applications like CATIA or Solidworks.
To import these models in your application, you will need a CAD Interoperability toolkit. Leveraging the 3D Modeler’s automatic feature recognition & removal, boolean and BRep deformation capabilities, you can make your user’s life quite easy.
We all remember that simulation assignment in school that seemed easy to finish at first but ended up taking days because there were too many unnecessary holes or fillets in the model that were slowing down your simulation and you had to manually remove them. Finally, one of the most important components in an FEM application is a mesher. A good mesher will be able to handle inaccuracies in the 3D model and produce reliable results on a consistent basis.


.jpg?width=450&name=Application%20Lifecycle%20Management%20(1).jpg)














